コンピュータの基礎数学として
扱う数の範囲があります。
全ての数を知っておく必要がありますで
分かりやすく解説していきます。
数の構成
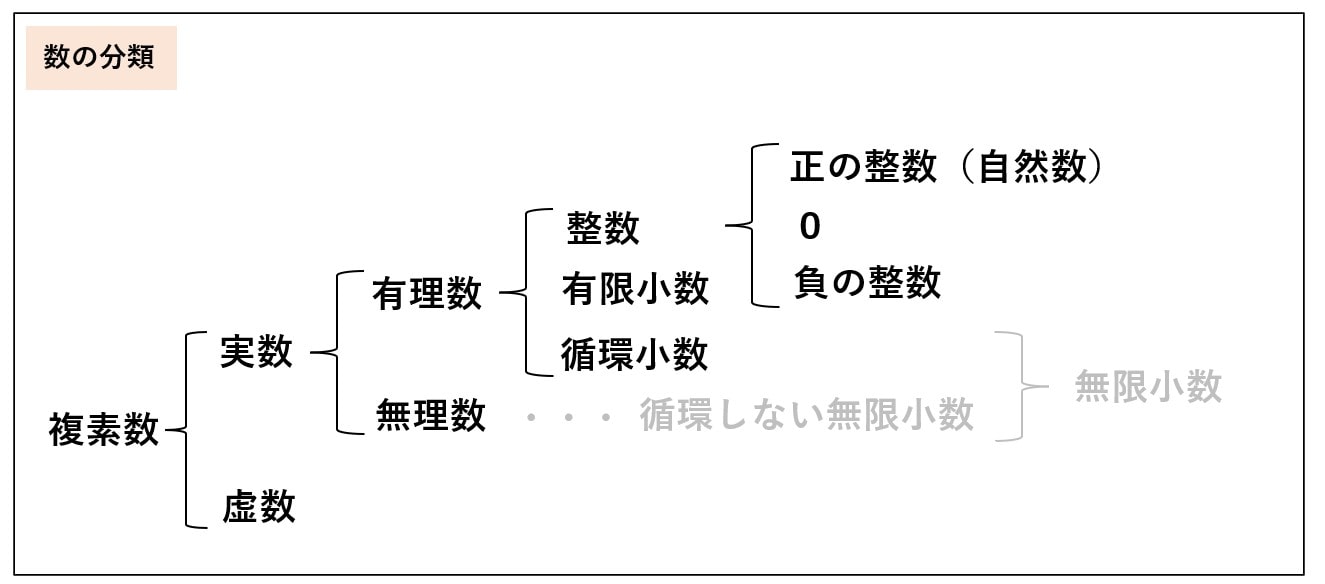
複素数
- 実数
数直線上に表せる数字。実際にあると確かめた数。 - 虚数
2乗して -1 になる数字。実際には存在しない数。
実数
- 有理数
分数で表せる数。 - 無理数
分数で表せない数。（数字の同じ並び方が循環しない無限小数）
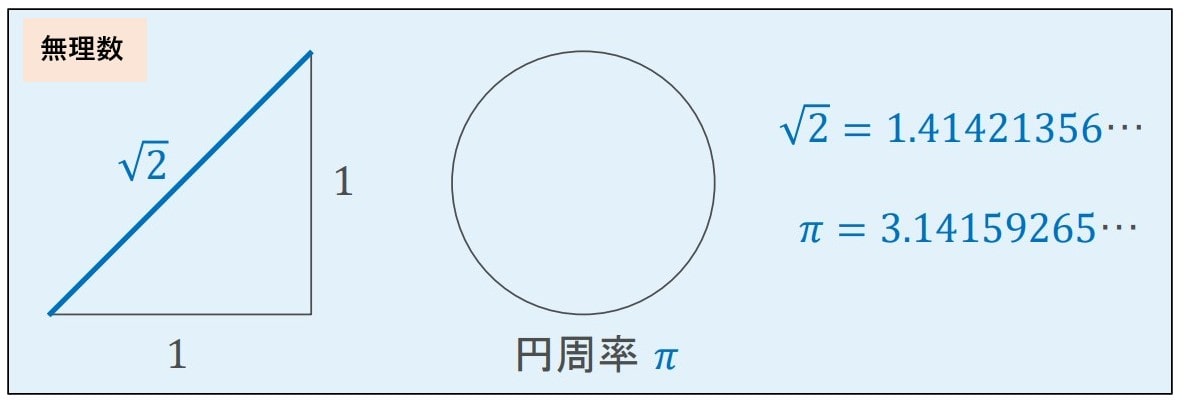
有理数
- 整数
少数でも分数でもない数。 - 有限小数
ある小数点以下に必ず終わりがある少数。 - 循環小数
ある小数点以下では、数字の同じ並び方が繰り返される小数。
整数
- 正の整数（自然数）
0よりも大きい整数で「1、2、3、…」という数。 - 0
正の整数でも負の整数でもない整数。 - 負の整数
0よりも小さい整数で「-1、-2、-3、…」という数。
計算方法
今後、コンピュータの世界では
「無理数の大小関係」や「無理数を有理化する」などの
計算方法を理解しておく必要があります。
そこで例題に解説を付け加えながら
紹介していきます。
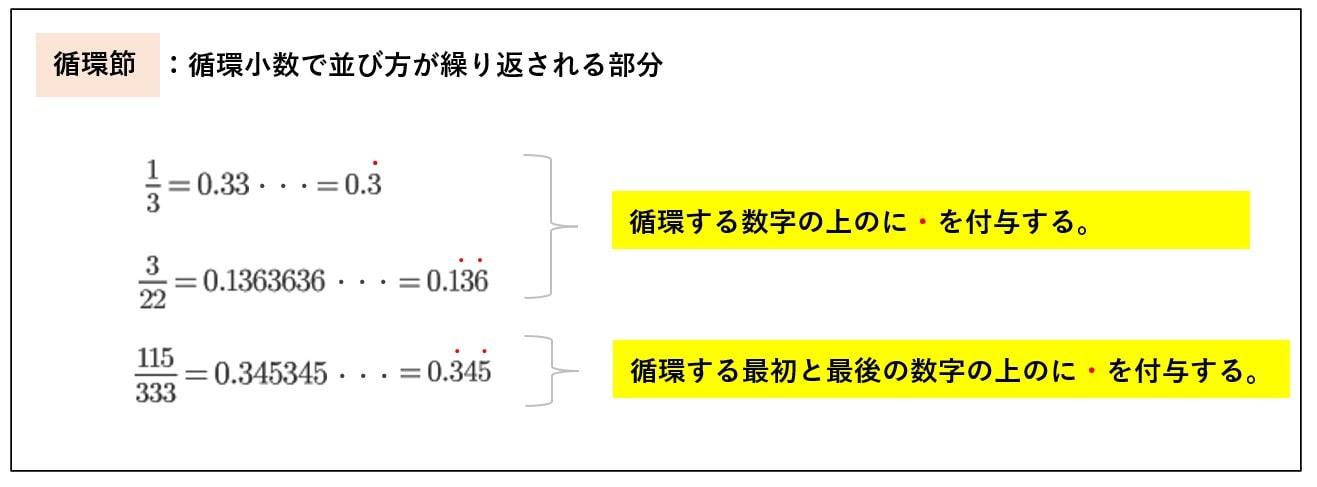
循環小数を簡単な表し方と分数への変換
循環小数を分数で表す方法を知っていると
とても便利ですし、色々と応用できるので覚えておきましょう。
二重根号の計算や分母がルートの場合の有理化
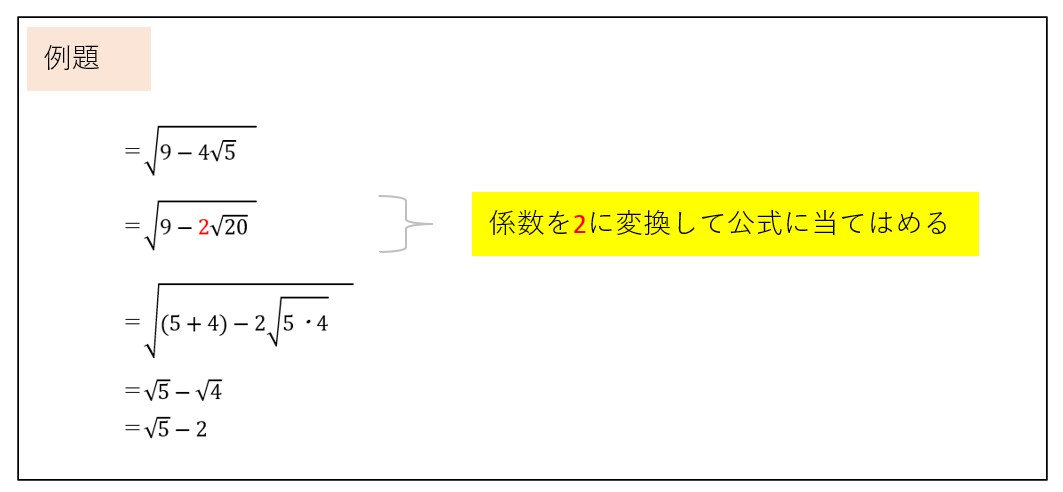
根号の中に根号があるものを2重根号といいます。
下記の公式を使います．
下記の公式が使える形になっていない場合は，
係数を2に変換して表します。
二重根号の公式
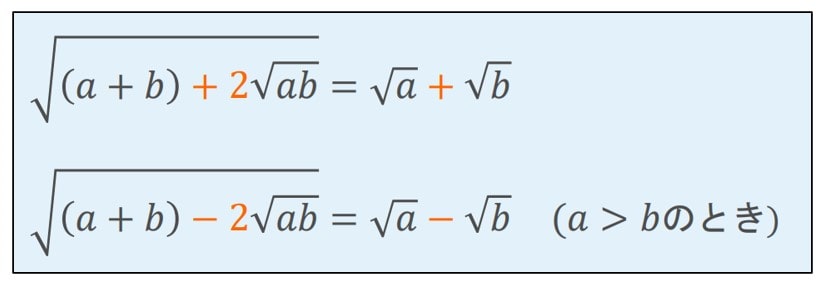
二重根号の計算
分母がルートの場合の有理化
分母がルートの場合の有理化（虚数）
複素数の構成についてと
無理数の計算方法について解説してきました。
また必要な部分がありましたら、
適宜、記事を修正追加していきます。
今の年収に満足していますか？
同じ契約金で業務委託していても
在籍している会社によって給料が違います。
今と同じスキル・業務内容でも
年収が変わるということです。
さらに以下を考慮すると
より年収アップにつながります。
- スキルセットと需要
- 経験と実績
- 業界や地域の市場価値
- 転職時の交渉スキル
転職先の企業の給与体系や
業界の標準的な給与水準を調査し、
給与のみでなく、
福利厚生やキャリア成長の機会、
ワークライフバランスなどの要素も
総合的に考慮することが重要です。
ITエンジニアの知識を効率よく身につけるには？
Kindle Unlimitedは、Amazonが提供する
月額定額制の電子書籍サービスを活用します。
また、Kindle Unlimitedには、
体験版が提供されています。
体験版では、一定期間（通常は30日間）に限り、
Kindle Unlimitedのサービスを
無料で利用することができます。
１．豊富な書籍のラインナップ
Kindle Unlimitedには、幅広いジャンルの書籍が
数十万冊以上含まれています。
小説、ビジネス書、自己啓発書、
学術書、漫画など、
様々なテーマや興味に合わせて
多彩な選択肢があります。
２．サービスの内容を体験
体験版では、Kindle Unlimitedの全ての機能を使いながら、
豊富な書籍のラインナップや
読書体験を体験することができます。
自身の読書の好みや
利用頻度に合うかどうかを確認できます。
３．解約が可能
体験版期間中にKindle Unlimitedのサービスに
満足しなかった場合、
期限内に解約することができます。
その場合、追加料金はかかりません。
Kindle Unlimitedでは
さまざまなジャンルの書籍が提供されています。
ITエンジニアとしてスキルを向上させたり
新しい技術を学んだりする際に、
Kindle Unlimitedは
便利な資源となるのでおすすめです。
この記事へのコメントはありません。